Рис.1. Схема установки Алана Аспекта (Аспэ) с соавторами.
Сигнал детектора PM0 от первого фотона ν1 открывает электронный затвор на время τ, в течение которого PM1 и PM2 готовы принять второй фотон ν2.
S - источник излучения, N1 - счетчик отраженных фотонов, N2 - счетчик прошедших фотонов, Nc - счетчик совпадений сигналов от PM1 и PM2
Сигнал детектора PM0 от первого фотона ν1 открывает электронный затвор на время τ, в течение которого PM1 и PM2 готовы принять второй фотон ν2.
S - источник излучения, N1 - счетчик отраженных фотонов, N2 - счетчик прошедших фотонов, Nc - счетчик совпадений сигналов от PM1 и PM2
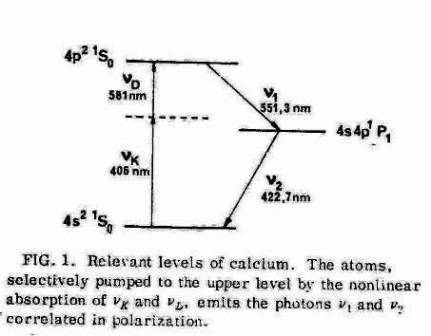
Рис.2
В ЧЕМ ОШИБСЯ АЛАН АСПЕКТ? О ПОПЫТКЕ ЭКСПЕРИМЕНТАЛЬНОГО ДОКАЗАТЕЛЬСТВА СУЩЕСТВОВАНИЯ ФОТОНА. Л.Р.
Ошибка Алана Аспекта (Аспэ) – в принятии недоказанного предположения, что в акте излучения всегда действует "целый" электрон. Само существование "электрона" есть гипотеза, которую необходимо проверять экспериментально, так же как и существование "фотона". Когда в излучении участвует лишь малая часть электронного облака, то испускается волновой цуг малой интенсивности, и вероятности совпадений отсчетов от такого цуга становятся слишком малыми.
В 1986 г. французские физики Гранжье, Роже и Аспэ провели решающий эксперимент, имеющий целью дать прямой ответ на ключевой вопрос квантовой физики – состоит свет из волновых цугов или из фотонов? [1].
Идея эксперимента (Рис.1) состояла в том, что излучение попадало на "расщепитель луча": полупрозрачное зеркало BS, которое делило его на две равные части, каждая их которых регистрировалась своим детектором (ФЭУ). Если свет состоит из частиц – фотонов, то такая частица может либо пройти через зеркало, либо отразиться от него, так что фотон не может попасть на оба ФЭУ сразу. Если же свет состоит из волновых цугов, то каждый цуг разделится зеркалом на две равные части, которые попадут на оба детектора одновременно.
Для реализации "однофотонного состояния" французские физики использовали каскадное излучение атомов кальция: при этом один за другим в течение времени τs испускаются два фотона с разными частотами ν1 и ν2. Первый из этих фотонов использовался как "запускающий", второй – как "рабочий".
Запускающий фотон вызывал импульс на детекторе PM0 , и этот импульс на время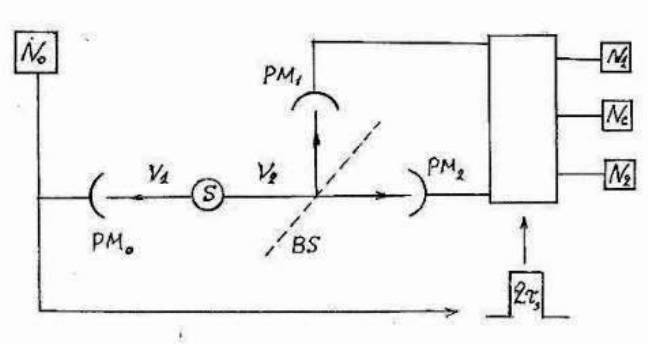
τ=2τs включал два других детектора: PM1 (для фотона, прошедшего через зеркало BS) и PM2 (для фотона, отразившегося от зеркала). Для того, чтобы детекторы могли различить запускающий и рабочий фотоны, перед PM0 ставился фильтр, пропускающий только частоту ν1, а перед PM1 и PM2 – фильтры, пропускающие только частоту ν2. Для подсчета корреляций сигналы с детекторов PM1 и PM2 поступали на счетчик совпадений. В случае справедливости фотонной гипотезы корреляции не должны иметь места, в случае отсутствия фотонов в волновом поле излучения – корреляции должны быть весьма частыми.
Скорости счета рабочих сигналов N1 и N2 связаны со скоростью счета запускающих сигналов N0 как:
N1 = ε1N0
N2 = ε2N0
где ε1 и ε2 – эффективности регистрации рабочих фотонов, главным образом определяемые квантовым выходом ФЭУ и телесным углом, под которым расходится рабочее излучение.
Эффективность регистрации запускающих фотонов определяется как:
N0 = ε0Nf
где Nf – число фотонов (или волновых цугов) в единицу времени: величина, которая непосредственно не может быть измерена.
Эффективности регистрации в данном эксперименте, согласно оценке авторов, были равны:
ε1 = ε2 = ε = 0,6х10(-3)
и соответственно:
N1 = N2 =N
Теоретическая оценка скорости счета совпадений NС от потока волновых цугов определялась как:
Nc = εε0 Nf (к + к²/2) = ε N(к + к²/2)
где к – среднее число световых импульсов (цугов или фотонов), поступающих на детектор PM0 за время τ=2τs. Второй член определяется случайными наложениями световых импульсов в течение этого промежутка, поэтому для корректности эксперимента необходимо было соблюдение условия к << 1.
При этом:
Nc = к ε N (1)
Наблюдавшаяся в эксперименте скорость счета совпадений оказалась почти на порядок меньше величины, рассчитанной по формуле (1) и целиком могла быть отнесена к случайным наложениям запускающих импульсов. Тем самым авторы считают доказанным, что свет представляет собой поток локализованных частиц – фотонов, которые делиться не могут.
В той же статье [1] авторы сообщают об интерференционном эксперименте с тем же самым излучением. То, что одно и то же поле излучения в одних экспериментах проявляет корпускулярные, а в других – волновые свойства, принимается как факт, не подлежащий объяснению и в таком качестве положенный в основу всей аксиоматики квантовой физики.
Вывод авторов заключается в том, что они доказали существование этого парадокса также и для излучения, представляющего собой совокупность однофотонных состояний.
Между тем, экспериментальное доказательство корпускулярной природы излучения, предложенное Аланом Аспэ с соавторами, содержит существенный изъян, на который до сих пор не было обращено достаточного внимания. Этот изъян заключается в том, что в основе методики эксперимента содержится молчаливое предположение фундаментального характера, которое само по себе нуждается в проверке. Если ставится вопрос о существовании корпускулярного фотона, то одновременно должен быть поставлен такой же вопрос о существовании корпускулярного электрона.
Две гипотезы: о локализованном электроне и о непрерывном электронном поле – приводят к принципиально разным выводам о структуре излучения. Если существует неделимый электрон, то в каждом акте излучения он участвует целиком, и при его переходах из более высокого состояния в более низкое испускаются цуги электромагнитного поля, интеграл от амплитуды которых всегда равен одной и той величине, которая может быть принята за 1 ("условие нормировки единичного электронного состояния"). Именно из этого предположения исходят Алан Аспект с соавторами, не подвергая обсуждению другую возможность, которая решающим образом влияет на интерпретацию их эксперимента.
Если же реальностью является не электрон-корпускула, но электронное поле в пространстве и времени, то "условие нормировки" (во всяком случае, для возбужденного электронного облака) перестает быть обязательным: на верхнем уровне может находиться лишь малая часть единичного электронного "облака". При переходе этого облака на нижний уровень будет испущен электромагнитный цуг столь же малой интенсивности, что приведет к уменьшению теоретической оценки вероятности совпадений отсчетов от одного такого цуга.
Полагая среднее значение заполненности верхнего уровня равным W, мы должны внести этот параметр в качестве сомножителя в оценку вероятности корреляций (1), а именно:
Nc = W к ε N (2)
Чтобы оценить значение параметра W в эксперименте Алана Аспэ с соавторами, обратимся к более ранним их статьям, в которых подробно описано устройство использованного ими источника излучения [2,3]. Возбуждение уровней каскадного перехода в атоме кальция производилось с помощью совместного действия двух лазеров, однако при этом имело место значительное рассогласование частот лазеров с частотами каждого отдельного перехода (Рис.2 или Fig.1 в [2]). Для нижней ступени каскада, испускающей "рабочий фотон", длина волны перехода составляла 422,7 нм, тогда как длина волны возбуждающего лазера была 406 нм. Отсюда получаем рассогласование частот:
∆ω = 2π∆ν = 1,9х10(14)гц.
Двухуровневая система под действием внешнего поля осциллирует таким образом, что часть электронной плотности периодически переходит с нижнего уровня на верхний и обратно (см., напр. [4], §5.2). При условии, что населенность нижнего уровня близка к 1, заселенность верхнего уровня определяется как:
W = (ΩR/Ω)²sin²(Ωt)
где
Ω = √(ΩR² + ∆ω²)
При условии ΩR << ∆ω выражение для заселенности приобретает вид:
W = (ΩR/∆ω)²sin²(∆ωt) (3)
Частота Раби ΩR определяется как:
ΩR =dabE/ћ
где dab – дипольный момент перехода, E - амплитуда возбуждающего поля.
Интенсивность лазерного излучения в рабочей зоне описываемого источника может быть оценена как J = 0,3х10³вт/см² и, соответственно, амплитуда
E = √ (2π J/с) = 0,5х10³в/см
Частота Раби при этом равна:
ΩR = 1,7х10(9)гц
Подставляя в (3) значения ΩR и ∆ω, получаем оценку населенности верхнего рабочего уровня (4s4p¹p1):
W ~ 10(-10) (4)
Если электрон есть неделимая корпускула, то населенность W определяет вероятность его пребывания на верхнем уровне, но в каждом акте излучения электрон переходит с верхнего уровня на нижний весь целиком, испуская электромагнитный цуг, естественным образом "нормированный" к 1.
Если же никаких корпускулярных электронов нет, а есть только непрерывное электронное поле, то величина W определяет, какая доля интегральной плотности единичного электронного состояния (условно принятая за 1), находится на верхнем уровне. Соответственно, интегральная интенсивность испущенного цуга составит такую же долю от единичного цуга, что равносильно уменьшению эффективности системы отсчета, в соответствии с (2).
В результате скорость счета совпадений, согласно (2), составит:
Nc/N = Wкε ~ 0,6х10(-13)
вместо Nc/N = 0,6х10(-3) по оценке Алана Аспэ с соавторами. Ясно, что при таких низких значениях эффективности никакие корреляции сигналов от единичного цуга не могли быть обнаружены.
Таким образом, для подтверждения или опровержения гипотезы о существовании фотонов с помощью методики Аспэ необходимо повторение эксперимента с соблюдением условия:
W ~ 1
Это может быть достигнуто устранением рассогласования частот, т.е. подбором лазеров с точным резонансом (∆ω << ΩR) для каждого из двух переходов каскада.
Принципиальный же вывод из наших рассуждений – в том, что вопрос о пространственной структуре электромагнитного поля должен решаться параллельно с вопросом о пространственной структуре электронного поля.
1. P.Grangier, G.Roger, A.Aspect. Experimental evidence for a photon anti-correlation effect on a beamsplitter. Europhys. Lett. Vol.1. Pp. 173-179, 1986.
2. A.Aspect, P.Grangier, G.Roger. Experimental Tests of Realistic Local Theories via Bell's Theorem.
Phys. Rev. Lett. Vol. 47, num. 7. Pp. 460-463, 1981.
3. A.Aspect, C.Imbert, G.Roger. Absolute measurement of an atomic cascade rate using a two photon coincidence technique application to the 4p²¹s0 – 4s4p¹p1 – 4s²¹s0 cascade of calcium exited by a two photon absorption.
Optics Comm. Vol. 31, num. 1. Pp. 46-52.
4. M.O.Scully, M.S.Zubairy. Quantum Optics. Cambridge Univ. Press, 1997.
Рус. перевод: М.О.Скалли, М.С.Зубайри. Квантовая Оптика. М. Физматгиз, 2003.
Л.Регельсон. 2009 г.
В 1986 г. французские физики Гранжье, Роже и Аспэ провели решающий эксперимент, имеющий целью дать прямой ответ на ключевой вопрос квантовой физики – состоит свет из волновых цугов или из фотонов? [1].
Идея эксперимента (Рис.1) состояла в том, что излучение попадало на "расщепитель луча": полупрозрачное зеркало BS, которое делило его на две равные части, каждая их которых регистрировалась своим детектором (ФЭУ). Если свет состоит из частиц – фотонов, то такая частица может либо пройти через зеркало, либо отразиться от него, так что фотон не может попасть на оба ФЭУ сразу. Если же свет состоит из волновых цугов, то каждый цуг разделится зеркалом на две равные части, которые попадут на оба детектора одновременно.
Для реализации "однофотонного состояния" французские физики использовали каскадное излучение атомов кальция: при этом один за другим в течение времени τs испускаются два фотона с разными частотами ν1 и ν2. Первый из этих фотонов использовался как "запускающий", второй – как "рабочий".
Запускающий фотон вызывал импульс на детекторе PM0 , и этот импульс на время
τ=2τs включал два других детектора: PM1 (для фотона, прошедшего через зеркало BS) и PM2 (для фотона, отразившегося от зеркала). Для того, чтобы детекторы могли различить запускающий и рабочий фотоны, перед PM0 ставился фильтр, пропускающий только частоту ν1, а перед PM1 и PM2 – фильтры, пропускающие только частоту ν2. Для подсчета корреляций сигналы с детекторов PM1 и PM2 поступали на счетчик совпадений. В случае справедливости фотонной гипотезы корреляции не должны иметь места, в случае отсутствия фотонов в волновом поле излучения – корреляции должны быть весьма частыми.Скорости счета рабочих сигналов N1 и N2 связаны со скоростью счета запускающих сигналов N0 как:
N1 = ε1N0
N2 = ε2N0
где ε1 и ε2 – эффективности регистрации рабочих фотонов, главным образом определяемые квантовым выходом ФЭУ и телесным углом, под которым расходится рабочее излучение.
Эффективность регистрации запускающих фотонов определяется как:
N0 = ε0Nf
где Nf – число фотонов (или волновых цугов) в единицу времени: величина, которая непосредственно не может быть измерена.
Эффективности регистрации в данном эксперименте, согласно оценке авторов, были равны:
ε1 = ε2 = ε = 0,6х10(-3)
и соответственно:
N1 = N2 =N
Теоретическая оценка скорости счета совпадений NС от потока волновых цугов определялась как:
Nc = εε0 Nf (к + к²/2) = ε N(к + к²/2)
где к – среднее число световых импульсов (цугов или фотонов), поступающих на детектор PM0 за время τ=2τs. Второй член определяется случайными наложениями световых импульсов в течение этого промежутка, поэтому для корректности эксперимента необходимо было соблюдение условия к << 1.
При этом:
Nc = к ε N (1)
Наблюдавшаяся в эксперименте скорость счета совпадений оказалась почти на порядок меньше величины, рассчитанной по формуле (1) и целиком могла быть отнесена к случайным наложениям запускающих импульсов. Тем самым авторы считают доказанным, что свет представляет собой поток локализованных частиц – фотонов, которые делиться не могут.
В той же статье [1] авторы сообщают об интерференционном эксперименте с тем же самым излучением. То, что одно и то же поле излучения в одних экспериментах проявляет корпускулярные, а в других – волновые свойства, принимается как факт, не подлежащий объяснению и в таком качестве положенный в основу всей аксиоматики квантовой физики.
Вывод авторов заключается в том, что они доказали существование этого парадокса также и для излучения, представляющего собой совокупность однофотонных состояний.
Между тем, экспериментальное доказательство корпускулярной природы излучения, предложенное Аланом Аспэ с соавторами, содержит существенный изъян, на который до сих пор не было обращено достаточного внимания. Этот изъян заключается в том, что в основе методики эксперимента содержится молчаливое предположение фундаментального характера, которое само по себе нуждается в проверке. Если ставится вопрос о существовании корпускулярного фотона, то одновременно должен быть поставлен такой же вопрос о существовании корпускулярного электрона.
Две гипотезы: о локализованном электроне и о непрерывном электронном поле – приводят к принципиально разным выводам о структуре излучения. Если существует неделимый электрон, то в каждом акте излучения он участвует целиком, и при его переходах из более высокого состояния в более низкое испускаются цуги электромагнитного поля, интеграл от амплитуды которых всегда равен одной и той величине, которая может быть принята за 1 ("условие нормировки единичного электронного состояния"). Именно из этого предположения исходят Алан Аспект с соавторами, не подвергая обсуждению другую возможность, которая решающим образом влияет на интерпретацию их эксперимента.
Если же реальностью является не электрон-корпускула, но электронное поле в пространстве и времени, то "условие нормировки" (во всяком случае, для возбужденного электронного облака) перестает быть обязательным: на верхнем уровне может находиться лишь малая часть единичного электронного "облака". При переходе этого облака на нижний уровень будет испущен электромагнитный цуг столь же малой интенсивности, что приведет к уменьшению теоретической оценки вероятности совпадений отсчетов от одного такого цуга.
Полагая среднее значение заполненности верхнего уровня равным W, мы должны внести этот параметр в качестве сомножителя в оценку вероятности корреляций (1), а именно:
Nc = W к ε N (2)
Чтобы оценить значение параметра W в эксперименте Алана Аспэ с соавторами, обратимся к более ранним их статьям, в которых подробно описано устройство использованного ими источника излучения [2,3]. Возбуждение уровней каскадного перехода в атоме кальция производилось с помощью совместного действия двух лазеров, однако при этом имело место значительное рассогласование частот лазеров с частотами каждого отдельного перехода (Рис.2 или Fig.1 в [2]). Для нижней ступени каскада, испускающей "рабочий фотон", длина волны перехода составляла 422,7 нм, тогда как длина волны возбуждающего лазера была 406 нм. Отсюда получаем рассогласование частот:
∆ω = 2π∆ν = 1,9х10(14)гц.
Двухуровневая система под действием внешнего поля осциллирует таким образом, что часть электронной плотности периодически переходит с нижнего уровня на верхний и обратно (см., напр. [4], §5.2). При условии, что населенность нижнего уровня близка к 1, заселенность верхнего уровня определяется как:
W = (ΩR/Ω)²sin²(Ωt)
где
Ω = √(ΩR² + ∆ω²)
При условии ΩR << ∆ω выражение для заселенности приобретает вид:
W = (ΩR/∆ω)²sin²(∆ωt) (3)
Частота Раби ΩR определяется как:
ΩR =dabE/ћ
где dab – дипольный момент перехода, E - амплитуда возбуждающего поля.
Интенсивность лазерного излучения в рабочей зоне описываемого источника может быть оценена как J = 0,3х10³вт/см² и, соответственно, амплитуда
E = √ (2π J/с) = 0,5х10³в/см
Частота Раби при этом равна:
ΩR = 1,7х10(9)гц
Подставляя в (3) значения ΩR и ∆ω, получаем оценку населенности верхнего рабочего уровня (4s4p¹p1):
W ~ 10(-10) (4)
Если электрон есть неделимая корпускула, то населенность W определяет вероятность его пребывания на верхнем уровне, но в каждом акте излучения электрон переходит с верхнего уровня на нижний весь целиком, испуская электромагнитный цуг, естественным образом "нормированный" к 1.
Если же никаких корпускулярных электронов нет, а есть только непрерывное электронное поле, то величина W определяет, какая доля интегральной плотности единичного электронного состояния (условно принятая за 1), находится на верхнем уровне. Соответственно, интегральная интенсивность испущенного цуга составит такую же долю от единичного цуга, что равносильно уменьшению эффективности системы отсчета, в соответствии с (2).
В результате скорость счета совпадений, согласно (2), составит:
Nc/N = Wкε ~ 0,6х10(-13)
вместо Nc/N = 0,6х10(-3) по оценке Алана Аспэ с соавторами. Ясно, что при таких низких значениях эффективности никакие корреляции сигналов от единичного цуга не могли быть обнаружены.
Таким образом, для подтверждения или опровержения гипотезы о существовании фотонов с помощью методики Аспэ необходимо повторение эксперимента с соблюдением условия:
W ~ 1
Это может быть достигнуто устранением рассогласования частот, т.е. подбором лазеров с точным резонансом (∆ω << ΩR) для каждого из двух переходов каскада.
Принципиальный же вывод из наших рассуждений – в том, что вопрос о пространственной структуре электромагнитного поля должен решаться параллельно с вопросом о пространственной структуре электронного поля.
1. P.Grangier, G.Roger, A.Aspect. Experimental evidence for a photon anti-correlation effect on a beamsplitter. Europhys. Lett. Vol.1. Pp. 173-179, 1986.
2. A.Aspect, P.Grangier, G.Roger. Experimental Tests of Realistic Local Theories via Bell's Theorem.
Phys. Rev. Lett. Vol. 47, num. 7. Pp. 460-463, 1981.
3. A.Aspect, C.Imbert, G.Roger. Absolute measurement of an atomic cascade rate using a two photon coincidence technique application to the 4p²¹s0 – 4s4p¹p1 – 4s²¹s0 cascade of calcium exited by a two photon absorption.
Optics Comm. Vol. 31, num. 1. Pp. 46-52.
4. M.O.Scully, M.S.Zubairy. Quantum Optics. Cambridge Univ. Press, 1997.
Рус. перевод: М.О.Скалли, М.С.Зубайри. Квантовая Оптика. М. Физматгиз, 2003.
Л.Регельсон. 2009 г.