
Jacques Lavau. The Zitterbewegung: key of the electron- photon scattering under the laws of Bragg and Compton
The Zitterbewegung: key of the electron-photon scattering under the laws of Bragg and Compton.
Jacques Lavau
lavaujac(at)club-internet.fr
Résumé
En 1927, Erwin Schroedinger avait presume prouver que la diffusion d'un photon gamma ou X par un electron etudiee par A. H. Compton, relevait de la loi de Bragg, par interférences sur les reseau d'ondes brogliennes. Toutefois cette demonstration etait prematuree et est erronee: seul le reseau d'ondes temporairement stationnaires dans le repere du centre d'inertie, resultant du battement entre les ondes Dirac-Schroedinger (= Zitterbewegung) de l'aller et du retour de l'électron, donne la bonne equidistance requise par la loi de Bragg. L'equidistance Bragg-Schroedinger est electromagnetique (Dirac 1930 -1957, Schroedinger 1930).
Les conditions de Bragg impliquent une largeur et une profondeur de l'ordre de la douzaine de distances interatomiques pour la largeur et la profondeur de l'interaction entre eectron et photon. C'est incompatible avec le mythe des "aspects corpusculaires", mythe pourtant hegemonique a ce jour.
Abstract
In 1927, Erwin Schrödinger presumed to have shown that the Compton scattering between an electron and a X photon, is relevant of the Bragg law, computed in the frame of the center of inertia. However, his demonstration could not use in 1927 the right equidistance for the Bragg law. Only the Dirac-Schrödinger electromagnetic waves, whose spatial and temporal frequencies are the double of the Broglian (spinorial) ones, provide the right equidistance for the Bragg law. The lattice of electromagnetic planes that reflect the photon, results of the superposition of incoming and departing electronic waves (Dirac 1930 -1957, Schrödinger 1930).
The Bragg conditions imply about a dozen of interatomic distances for both the depth and the width of the interacting photon and electron. So once again, there are no "corpuscular aspects" in the real physical world. Only waves, emitters and absorbers.
Required
In the frame of the laboratory, the results are well known (Greiner 1981) :
Conservation of the energy:
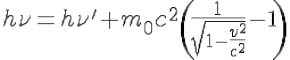
Conservation of the linear momentum on axis of the incident photon :
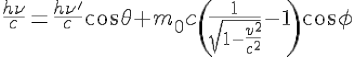
and on the perpendicular axis, where the linear momentum is null :
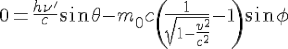
Solving these equations, one obtains
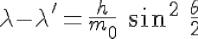
Demonstration in the frame of the center of inertia
We perform again the calculation, but in the frame of the center of inertia. Of course, one can not experiment in this frame, as its occurrence is at random : one can not choose by advance the scattering deviation, and we remain prisoners of the frame of the laboratory.
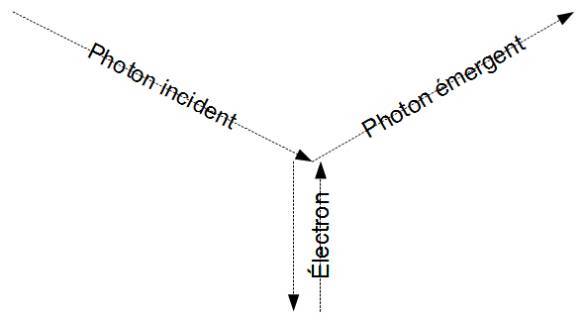
There the calculation is far more straightforward and simple : the photon does not change its frequency, nor its energy, only its course. Set it comes from the left, downing by the angle
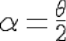
and then upping by the same angle. The electron does not change of kinetic energy, just the sign of its speed. We neglect its binding energy to the solid.
Momentum on z'z transmitted by the photon to the electron: (-)
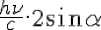
(sign - : descending if axis z'z is vertical and upping).
Balanced by the change of momentum of the electron
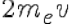
first calculation, non relativistic), or relativistic form.
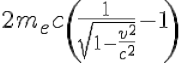
Hence the speed of incoming and outcoming of the electron:
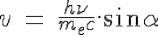
(non relativistic)
Hence its phase celerity:

Now we know the intrinsic period of the electron,
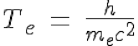
Hence its broglian wavelength:
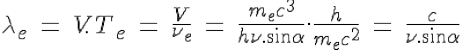
It is noteworthy that this wavelength does not depend on the electron mass, and would be the same for any particle, charged or not, which is subject to Compton scattering. It does not depend either of the Planck's constant. It depends only of the angle of deviation of the photon, and of its period or wavelength (evaluated in the frame of the center of inertia) before and after the scattering.
On the model of refraction and reflection on a dioptre, we calculate the emission of this mirror for photon, which is this electron.
The horizontal part, on x'x is unvarying. Its wavelength is
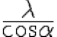
The wavelength of the penetrating part, as well of the reflected part of the photon is
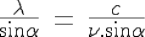
These two wavelengths, of the rebouncing electron, and of the reflected part of the photon, are equal.
Up to now, the calculus has not given anything on the spatial extension of the X photon and electron. We only know, by practice of radiocrystallography with molybdenum
ray in metallurgy (and copper and cobalt ray in metallurgy (and copper and cobalt
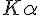
in mineralogy), that its wavelength is about the interatomic distances in metals, and that the valency electrons are weakly bound, and little localized, extending on ten or twenty interatomic distances (and the phonons are even less localized). Together with geometric constraints on diffraction on the atomic planes, this compels us to conclude that both the electron and the photon are large and deep of tens of interatomic distances, all along the Compton interaction.
Numerical calculus, with the mean
 ray of molybdenum:
ray of molybdenum:
Let us take a case of strong deviation of the photon, twice 30°, that is
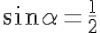
The mean wavelength of incident ray is 0.070926 nm
Hence the external projection (external to the propagation of the electron):
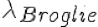
= 0,070926nm x2 = 0,141852 nm
Hence the speed of the electron:
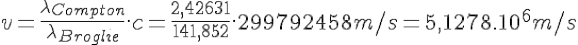
is a non-relativistic speed: 1.7% of c. It would even less relativistic with low deviations.
Then to the frame of the incoming electron...
Passing to the frame of the incoming electron, not very different from the frame of the laboratory, one should retrieve the experimental formula of Arthur Compton. However with the following causes of error :
Jacques Lavau
lavaujac(at)club-internet.fr
Résumé
En 1927, Erwin Schroedinger avait presume prouver que la diffusion d'un photon gamma ou X par un electron etudiee par A. H. Compton, relevait de la loi de Bragg, par interférences sur les reseau d'ondes brogliennes. Toutefois cette demonstration etait prematuree et est erronee: seul le reseau d'ondes temporairement stationnaires dans le repere du centre d'inertie, resultant du battement entre les ondes Dirac-Schroedinger (= Zitterbewegung) de l'aller et du retour de l'électron, donne la bonne equidistance requise par la loi de Bragg. L'equidistance Bragg-Schroedinger est electromagnetique (Dirac 1930 -1957, Schroedinger 1930).
Les conditions de Bragg impliquent une largeur et une profondeur de l'ordre de la douzaine de distances interatomiques pour la largeur et la profondeur de l'interaction entre eectron et photon. C'est incompatible avec le mythe des "aspects corpusculaires", mythe pourtant hegemonique a ce jour.
Abstract
In 1927, Erwin Schrödinger presumed to have shown that the Compton scattering between an electron and a X photon, is relevant of the Bragg law, computed in the frame of the center of inertia. However, his demonstration could not use in 1927 the right equidistance for the Bragg law. Only the Dirac-Schrödinger electromagnetic waves, whose spatial and temporal frequencies are the double of the Broglian (spinorial) ones, provide the right equidistance for the Bragg law. The lattice of electromagnetic planes that reflect the photon, results of the superposition of incoming and departing electronic waves (Dirac 1930 -1957, Schrödinger 1930).
The Bragg conditions imply about a dozen of interatomic distances for both the depth and the width of the interacting photon and electron. So once again, there are no "corpuscular aspects" in the real physical world. Only waves, emitters and absorbers.
Required
In the frame of the laboratory, the results are well known (Greiner 1981) :
Conservation of the energy:
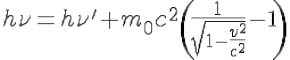
Conservation of the linear momentum on axis of the incident photon :
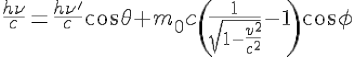
and on the perpendicular axis, where the linear momentum is null :
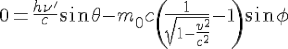
Solving these equations, one obtains
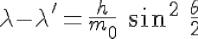
Demonstration in the frame of the center of inertia
We perform again the calculation, but in the frame of the center of inertia. Of course, one can not experiment in this frame, as its occurrence is at random : one can not choose by advance the scattering deviation, and we remain prisoners of the frame of the laboratory.

There the calculation is far more straightforward and simple : the photon does not change its frequency, nor its energy, only its course. Set it comes from the left, downing by the angle
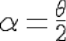
and then upping by the same angle. The electron does not change of kinetic energy, just the sign of its speed. We neglect its binding energy to the solid.
Momentum on z'z transmitted by the photon to the electron: (-)
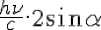
(sign - : descending if axis z'z is vertical and upping).
Balanced by the change of momentum of the electron
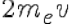
first calculation, non relativistic), or relativistic form.
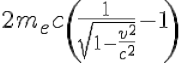
Hence the speed of incoming and outcoming of the electron:
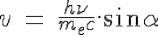
(non relativistic)
Hence its phase celerity:

Now we know the intrinsic period of the electron,
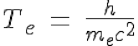
Hence its broglian wavelength:
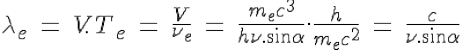
It is noteworthy that this wavelength does not depend on the electron mass, and would be the same for any particle, charged or not, which is subject to Compton scattering. It does not depend either of the Planck's constant. It depends only of the angle of deviation of the photon, and of its period or wavelength (evaluated in the frame of the center of inertia) before and after the scattering.
On the model of refraction and reflection on a dioptre, we calculate the emission of this mirror for photon, which is this electron.
The horizontal part, on x'x is unvarying. Its wavelength is
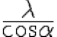
The wavelength of the penetrating part, as well of the reflected part of the photon is
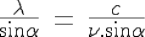
These two wavelengths, of the rebouncing electron, and of the reflected part of the photon, are equal.
Up to now, the calculus has not given anything on the spatial extension of the X photon and electron. We only know, by practice of radiocrystallography with molybdenum
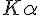
ray in metallurgy (and copper and cobalt ray in metallurgy (and copper and cobalt
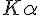
in mineralogy), that its wavelength is about the interatomic distances in metals, and that the valency electrons are weakly bound, and little localized, extending on ten or twenty interatomic distances (and the phonons are even less localized). Together with geometric constraints on diffraction on the atomic planes, this compels us to conclude that both the electron and the photon are large and deep of tens of interatomic distances, all along the Compton interaction.
Numerical calculus, with the mean
 ray of molybdenum:
ray of molybdenum:Let us take a case of strong deviation of the photon, twice 30°, that is
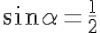
The mean wavelength of incident ray is 0.070926 nm
Hence the external projection (external to the propagation of the electron):
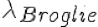
= 0,070926nm x2 = 0,141852 nm
Hence the speed of the electron:
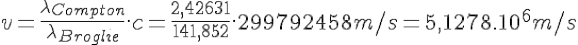
is a non-relativistic speed: 1.7% of c. It would even less relativistic with low deviations.
Then to the frame of the incoming electron...
Passing to the frame of the incoming electron, not very different from the frame of the laboratory, one should retrieve the experimental formula of Arthur Compton. However with the following causes of error :
1. A valency electron is not at rest, but at Fermi level and Fermi speed in the metal.
2. And we have neglected its bounding energy, in metallic bounding.
.
The first mentioned is the main cause of error and enlarging of the Compton scattering, the Fermi Level, plus the fact that the
 X ray is a doublet.
X ray is a doublet. The principle objection is that we have just stated the exchange in wave vectors, without establishing the physics of the interaction
Vertical component of the gamma incoming wave vector = electronic wave vector outcoming.
So the physics of the interaction remains unknown at this step of the calculus.
The failure is guaranteed if we extrapolate to microphysics the usual macrophysical scheme, with a massive object that slows, then restarts in the opposite direction, with finite acceleration all during the interaction. In 1926 (Schrödinger 1926) Erwin Schrödinger had showed the path, considering emission of a photon as the beat of atomic (or molecular) electronic wave between its final and initial state. Here again, it is a matter of beating between the initial upping state and final downing state of the electron. During the beating, an intermediate state contains a stationary broglian wave, to dispatch among four Dirac's components, whose two are antichrones, with negative frequencies.
Here is obvious another constraint, but we do not know whether it has been experimentally proved (nor whether it can be experimentally tested): the electrical polarization is necessarily in the plane of the drawing.
Bragg's condition and Zitterbewegung
The Bragg condition in radiocrystallography :
Set d is the interreticular distance,
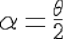
is the angle of the incident ray on the reticular plane, or half of the total deviation,
the wavelength of the incident ray, and n an integer, order of the reflection:

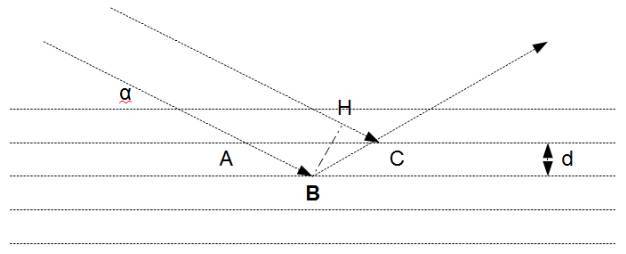
Demostration : incoming with α on the reticular planes AB etc., the monochromatic wave reflected by the next plane has a path difference equal to BC - HC. The first reflexion only exists if BC - HC is exactly one wavelength. In the isosceles triangle ABC,
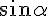 d = BС
d = BСThough in the rectangular triangle BCH,
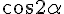 CH = BC
CH = BC The pass difference between the two waves is BC - CH =
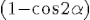 BC
BC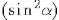 =2BC
=2BC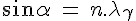
Nevertheless, the broglian wavelength, as calculated above, which was the only known and used by Erwin Schroedinger in 1927 (Schroedinger 1927) only gives us the reflection of second order:
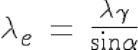
Its is a weak reflection, though one should observe the main reflection at order 1, which is never observed (and which would violate the laws of conservation of energy-momentum)...
It remains only one outlet: to consider the stationary electromagnetic wave, with doubled temporal and spatial frequencies, the Zitterbewegung, the trembling motion discovered by Erwin Schrödinger in 1930 (Schrödinger 1930, Dirac 1930, 1958) according to the Dirac equation, which yields the right Bragg reticular equidistance, exactly d!
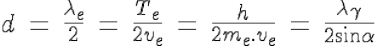
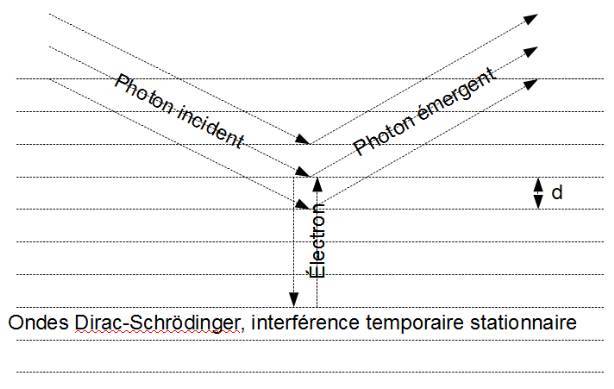
Conclusions
Only the spatial frequency of the Zitterbewegung, the trembling motion discovered by Erwin Schrödinger in 1930, stationary during the reflection of the electron on the photon, satisfies the Bragg condition for a first order reflex, and gives exactly the Compton scattering of the incoming photon.
If you compare the two Nobel lectures of Dirac and Schrödinger in 1933, only Dirac mentions some results of Schrödinger on the Zitterbewegung: exactly this one... This remains a heavy secret in the Göttingen-København sect. These works and results are kept secret and hidden in every handbooks.
Our aim was to exhibit the physical and undulatory mechanism that lies under the Compton scattering. Goal accomplished: Only the equidistance of the temporarily stationary Dirac-Schrödinger waves satisfies the Bragg condition, for first order diffraction. The fact that Erwin Schroedinger did not correct himself in 1930 his error of 1927, gives the measure of the meticulous demoralization obtained on him by Bohr and Heisenberg (Segre 1984, Selleri 1986). Not the slightest allusion on that in his Nobel lecture in 1933, where the two last pages deny all the work described in the previous pages.
Quod Erat Demonstrandum!
Other consequences:
Knowing the spatial extent of a conduction electron at the Fermi level, the Compton interaction electronphoton only imposes to this apex a modest constraint of pinching of the Fermat's taperings, about some nanometers, when the reactional conditions on the previous emitter and following absorber, as well for the electron and the X photon can eventually be more pinched; the details depend on the precise physics of these emitters and absorbers.
The electron returns under physical laws, individually. Well, it may sound a dullness, however under the standard mythology (Greiner 1935, Charpak, Omnes 2004, Hawking, Mlodinow 2010), each quanton individually escaped to any physical laws. Only in great numbers, it rejoined statistically some physical laws, by the mysterious mean of a physical mechanism remaining totally mysterious, though postulated however.
It is no more necessary to postulate some exorbitant physical mechanism, never observed and never theorized, that could perform the magic transmutation of an electron or a photon into some "small corpuscle", or worse: "punctual corpuscle".
Thanks
Thanks to Lev Lvovitch Regelson, who accomplished an unprecedented act of withstand: let accessible to all a paper from Erwin Schrödinger, at http://www.regels.org/Compton-Schrodinger.htm
Bibliography and references
Compton 1923: Arthur H. Compton. A quantum theory of the scattering of X-rays by light elements. The Physical Review. May 1923, vol 21, n°5.
P.A.M. Dirac. The Principles of Quantum Mechanics. Oxford University Press, ed 1958. § 69.
Greiner 1981: W. Greiner. Relativistic Quantum Mechanics ; Wave Equations. Springer Verlag, ed. 1997.
Schroedinger 1926: An Undulatory Theory of the Mechanics of Atoms and Molecules. The Physical Review, 28, (1926), 1049-1070
Schroedinger 1927: E. Schrödinger. Über den Comptoneffect. Annalen der Physik. IV. Folge, 62. http://www.regels.org/Compton-Schrodinger.htm
Adresses given by: Lev Lvovitch Regelson. Compton effect: Schrödinger's treatment in: The Science Forum - Scientific Discussion and Debate. http://www.thescienceforum.com/viewtopic.php?p=235655, link changed to: http://www.thescienceforum.com/physics/18025-compton-effect-schroedingerstreat ment.html
Schrödinger 1930: Uber die kräftefreie Bewegung in der relativistischen Quantenmechanik. Sitzungsberichte der Preußischen Akademie der Wissenschaften. Physikalisch-mathematische Klasse, (1930), 418-428
Schrödinger 1933: Nobel Lecture, December 12, 1933. The Fundamental Idea of Wave Mechanics. http://www.nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-lecture. html http://www.nobelprize.org/nobel_prizes/physics/laureates/1933/schrodinger-lecture. pdf Segrè 1984: Emilio Segre. Les physiciens modernes et leurs découvertes. Fayard, Paris 1984.
Selleri 1986: Franco Selleri. Le grand débat de la théorie quantique. Flammarion, Paris 1986.
Anti-references, a bunch of what not to do (collected at: http://citoyens.deontolog.org/index.php/topic,887.0.html):
Georges Charpak et Roland Omnes. Soyez savants devenez prophetes. Ed. Odile Jacob, Paris, juillet 2004. Pages 87 - (92 ?).
Wolgang Greiner 1935. Quantum Mechanics, Special Chapters, pp 365-367. Springer Verlag, ed. 1998.
Stephen Hawking, Leonard Mlodinow 2010. The Grand Design. Bentham Books, 2010.

