Eur. J. Phys. 7 (1986)
Department of Physics and J. Stefan Institute, University of Ljubljana. 61111 Ljubljana, Yugoslavia.
Received 12 August 1985, in final form 30 October 1985
Department of Physics and J. Stefan Institute, University of Ljubljana. 61111 Ljubljana, Yugoslavia.
Received 12 August 1985, in final form 30 October 1985

Ervin Schrödinger
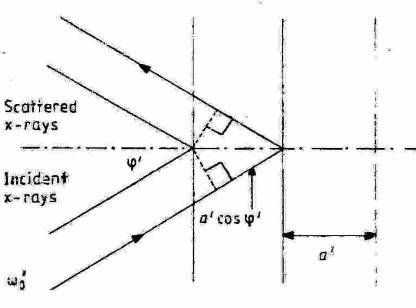
Figure 1. The Bragg condition in the “temporal interaction frame” S': specular reflection of the incident X-rays on the periodic probability density.
*In special relativity the phase of a wavefunction is a scalar product of two four-vectors and thus it is Lorentz invariant. This is not the case in Galilean relativity. Therefore a relativistic consideration appears to be inevitable. With some care, however, a nonrelativistic approximation of the above equations can be obtained (Strnad 1986a).
**It should be mentioned in passing that a somewhat similar situation is encountered in the free-electron laser in which an ultrarelativistic electron beam is directed parallel to a laser beam through a spatially periodic wiggler magnetic field. In the laboratory frame the laser field has a wavelength much shorter than the period of the wiggler field but both frequencies are equal as a result of the Doppler shift due to the motion of electrons. Bambini et al (1979) have introduced a reference frame moving in the direction of the electron beam in which the periodic structure is described by a pseudo-radiation field and the process as stimulated scattering, i.e. scattering at resonance, of the pseudo-radiation field into the true radiation field. This frame has some features in common with the “temporal interaction frame” S'. However, its velocity in the laboratory frame √ [c(1 – 2λ / L)] depends on the period of the static wiggler field L and the laser wavelength λ but not on the velocity of electrons.
The Compton effect — Schödinger's treatment
J. Strnad
Abstract. The Compton formula is obtained in a semiclassical approximation due to Schrödinger. X-rays are treated within classical electrodynamics and electrons within quantum mechanics. The superposition of the wavefunctions of the incident and recoiling electron sets up a moving periodic probability density. Incident x-rays are specularly reflected from this pattern. The results are transformed back into the original rest frame of the electron by the Doppler shift equation. Finally, some remarks pertaining to the philosophy of physics are added.
Zusammenfassung . Die Comptonsche Formel wird in einer von Schrödinger vorgeschlagenen semiklassischen Näherung gewonnen. Röntgenstrahlen werden in der klassischen Elektrodynamik und Elektronen in der Quantenmechanik beschrieben. Die Superposition der Wellenfuktionen des einfallenden und zurückgestossenen Elektrons gibt eine bewegte periodische Wahrscheinlichkeitsdichle. Einfallende Röntgenstrahlen werden an diesem Muster gebeugt. Die Resultate werden mittels der Gieichung für die Doppler-Verschiebung zurüuck in das Bezugssystem des ursprünglich rahenden Elektrons transformiert. Abschliessend werden einige wissenschaftstheoretische Bemerkungen geäussert.
1. Introduction
In textbooks of introductory quantum physics the light quantum, or photon, picture is usually introduced by studying the photoelectric effect. A photon of radiation with angular frequency ω has energy ћω. This conclusion is corroborated by considering the Compton effect as an elastic collision of a photon with a free electron at rest, A photon with energy ћω has momentum ћω/c.
Abstract. The Compton formula is obtained in a semiclassical approximation due to Schrödinger. X-rays are treated within classical electrodynamics and electrons within quantum mechanics. The superposition of the wavefunctions of the incident and recoiling electron sets up a moving periodic probability density. Incident x-rays are specularly reflected from this pattern. The results are transformed back into the original rest frame of the electron by the Doppler shift equation. Finally, some remarks pertaining to the philosophy of physics are added.
Zusammenfassung . Die Comptonsche Formel wird in einer von Schrödinger vorgeschlagenen semiklassischen Näherung gewonnen. Röntgenstrahlen werden in der klassischen Elektrodynamik und Elektronen in der Quantenmechanik beschrieben. Die Superposition der Wellenfuktionen des einfallenden und zurückgestossenen Elektrons gibt eine bewegte periodische Wahrscheinlichkeitsdichle. Einfallende Röntgenstrahlen werden an diesem Muster gebeugt. Die Resultate werden mittels der Gieichung für die Doppler-Verschiebung zurüuck in das Bezugssystem des ursprünglich rahenden Elektrons transformiert. Abschliessend werden einige wissenschaftstheoretische Bemerkungen geäussert.
1. Introduction
In textbooks of introductory quantum physics the light quantum, or photon, picture is usually introduced by studying the photoelectric effect. A photon of radiation with angular frequency ω has energy ћω. This conclusion is corroborated by considering the Compton effect as an elastic collision of a photon with a free electron at rest, A photon with energy ћω has momentum ћω/c.
This procedure is misleading since it implies that the photon picture is exclusive in explaining the Compton effect. Therefore it is worthwhile to discuss other methods which describe the effect without introducing photons explicitly (Dodd 1983, Kidd et al 1985, Kuhn and Stöckler 1985).
Recently, Dodd (1983) in this journal revisited Compton's (1923) treatment within classical electrodynamics, elaborating it from the didactical point of view. Another treatment of the Compton effect is due to Schrödinger (1927). This treatment is seldom mentioned in textbooks, and then preferably in terms of momentum and energy conservation (e.g. Döring 1973). In § 2 a straightforward and simple relativistic calculation is presented which is, in a sense, a complementary sequel to Dodd's and uses similar tools. Section 3 contains a brief discussion of the theoretical background of the 'treatments of the Compton effect.
2. A calculation in Schrödinger's spirit
At the beginning of his paper Schrödinger (1927) wrote: “According to the wave theory of light all changes in frequency and wave normal can he predicted, as is well known, on the basis of very simple and general considerations on the phase, without going into any detail of the phenomenon... If the assumption is correct that with the de Broglie waves we have at hand a tool, equivalent to wave optics, for the treatment of those phenomena that were formerly understood exclusively as motions of particles, we should expect and demand that on the basis of simple phase considerations of the stated kind one should understand the changes in direction and frequency of the aether wave in the Compton effect connected with the velocity change of the electron”.
Schrödinger argued that x-rays can be diffracted on a standing “charge density” wave, due to the incident and recoiling electron, just as light is diffracted on a standing wave of ultrasound (Born and Wolf 1959).
Since the charge density is not stationary m the laboratory frame of reference the Doppler effect has to be taken into account.
Let the x axis of the laboratory frame S be the direction of the recoiling electron. Initially the electron has energy mc² and momentum 0 and after recoil energy γmc² and momentum γβmc. Here m is its rest mass, v its velocity after recoil, c the velocity of light β=v/c and γ=1/√(1 – β² ).
In the laboratory frame the superposition of the wavefunctions of the incident and recoiling electron is
ψ = ½ exp (-i mc² ) + ½ exp [i mcγ (βx – ct)/ћ]
For the sake of simplicity the coefficients have been taken to be real, and equal. The corresponding probability density
ψ*ψ = cos² [(Px – Wt)/2ћ]
with Wt = mc² (γ –1) and P = γβmc, is not stationary in the laboratory frame owing to the term Wt/2ћ. We can, however, find an inertial frame of reference S', the origin of which is moving with velocity vo = βo c along the x axis and in which the probability density is stbtionary*.
The condition that the probability density is stationary is
W' = γo (W – βo cP) = 0
Therefrom one obtains
βo = √[(γ –1)/(γ +1)] γo = √[½(γ +1)]
and
P' = γo (P – βoW/c)= √ mc[2(γ –1)]
In the “temporal interaction frame” S' the incident and the recoiling electron have opposite momenta**.
The spatial period, i.e. the distance between adjacent planes of maximum probability density, can be inferred from
ψ*ψ' = cos² (P'x'/2ћ) by P'a'/2ћ = π
In turn a de Broglie-type relation follows
a' = h/P'
Now we state, in frame S', the Bragg condition (figure 1)
2a' cos φ' = n λ'o (1)
where λ'o = 2πc/ωo is the wavelength, ωo the angular frequency, and φ' the angle with respect to the x' axis of the incident X-rays in frame S'. We put n = 1 since a Fourier transform shows that at diffraction on a cosine-square grating only maxima of the order 0 and ±1 survive (Hecht and Zajac 1979).
Condition (1) can be rewritten as
ω'o cos φ' = (mc² ћ)γo βo = ωo√½ (γ –1) (2)
with the Compton angular frequency
ωo = mc² /ћ
The condition (2) can be interpreted as momentum conservation in frame S'. The total momentum, made up of the momentum of the electron and the momentum of the radiation field, before scattering is equal to the total momentum after scattering:
x' components:
– γo βo mc + (ћω'o/c) cos φ'
γo βo mc – ( ћω'o/c) cos φ'
y' components:
(ћω'o/c) sin φ'
(ћω'o/c) sin φ'
Energy in frame S' is conserved automatically since neither the energy of the electron nor the energy of the radiation field is changed at scattering,
Now we transform back to the laboratory frame S. As already stated the electron four-momentum before and after scattering
(γomc, – γo βo mc, 0, 0) and (γomc, γo βo mc, 0, 0)
respectively, goes over into
(mc, 0, 0,0) and (γmc, γβmc, 0, 0)
The four-dimensional wavevector of the radiation field before and after scatteiing, [(ω'o/c, (ω'o/c) cos φ', (ω'o/c) cos φ', 0]
and
[(ω'o/c, – (ω'o/c) cos φ', (ω'o/c) cos φ', 0]
respectively, by the inverse Lorentz transformation known from the Doppler effect (see e.g. Møller 1972)
ωo = γo ω'o (1 + βo cos φ')
ωo cos φ = γo ω'o (cos φ' + βo)
ωo sin φ = ω'o sin φ'
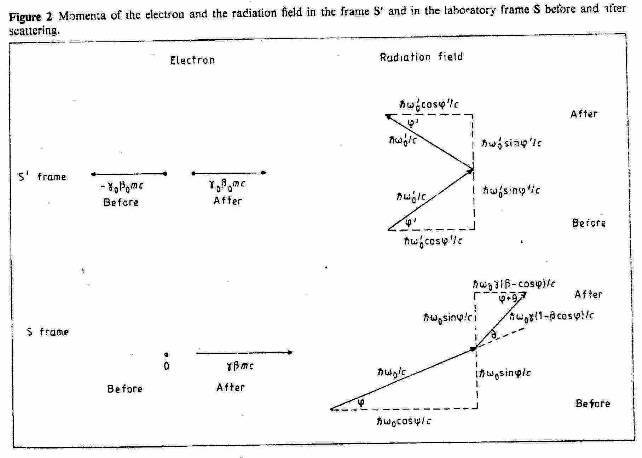
becomes (figure 2)
[γo ω'o (1 + βo cos φ')/c, γoω'o(cos φ' + βo), ω'o (sinφ' / c, 0)]
=[ωo/c, ωo cosφ / c, ωo cosφ / c, 0]
and
[γo ω'o (1 – βo cos φ')/c, γo ω'o (βo – cos φ' ), ω'o (sinφ' / c, 0]
= [γωo (1 – cos φ)/c, ωo(β – cos φ)/c, ωo sinφ / c, 0]
In the last step we have expressed ω'o and φ' with ωo and φ through the Lorentz transformation
ω'o = γo ωo (1 – βo cos φ)
ω'o cos φ' = γo ωo (cos φ – βo)
 and used relations connecting βo and γo with β and γ . The same transformation translates equation (2) into the Bragg condition in the laboratory frame S:
and used relations connecting βo and γo with β and γ . The same transformation translates equation (2) into the Bragg condition in the laboratory frame S: ωo cos φ = (ωo + ωc) βo (4)
In the laboratory frame S energy and momentum are conserved, as one expects: for energy
mc² + ћωo = γmc² + γћωo(1 – β cos φ)
for momentum:
x components:
ћωo cos φ/c = γβmc + γћωo (β – cos φ)/с (5)
y components:
ћωo sin φ/c = ћωo sin φ/c
The equations can be proven directly using relations connecting βo and γo with β and γ and condition (4).
After introducing the scattering angle of the X-rays. θ and some manipulations we obtain the well known equation for the angular frequency of the scattered x-rays in the S frame
ω = ωo / [1 + (ωo / ωc)(1 – cos θ)]
Therewith we have to take account of introducing the reference frame S' with respect to the recoiling electron. One can proceed either formally by writing down the equations
[γ ωo (β – cos φ)] / c = [ ω cosφ + θ)]/c
(ωosin φ)/c = [ωo sin (φ + θ)] /c
or by demanding, as is done usually, the conservation of momentum components in the direction of the incident x-rays and normally to this direction.
3. Discussion
Schrödinger's treatment of the Compton effect reminds us that a theory cannot be deduced directly from experiment; the same result may even be explained by two different theories. It also shows that the reaction of a physicist to empirical data is often governed by his common belief. It is well known that Schrödinger disliked 'quantum jumps' and preferred the concept of continuous waves.
The Compton effect can be tackled in different theoretical approaches at different levels of sophistication The first level is represented by Compton's treatment, the second one by Schrödinger's treatment and the third by quantum electrodynamics (QED). Let us' note briefly the main characteristics of the three approaches. Certainly QED cannot be considered in introductory quantum physics. Nevertheless, one should be aware that by describing the Compton effect as an elastic collision of a photon with an electron the basic features of QED are exploited. In QED photons are introduced as excitations of the radiation field (Strnad 1986b) and it should be taken into account that it makes no sense to ascribe to them a position: a photon belongs to the entire volume in which the field has been quantised.
Schrödinger's treatment belongs to the realm of the semiciassical approximation in which particles with rest mass are described within quantum mechanics and the radiation field within classical electrodynamics. In this approximation there is no room for photons. „n spite of this, many elementary processes can be successfully described in this approximation, e.g. the photoelectric effect, absorption. stimulated emission. The
 fact that this is not the case for some processes, e.g. spontaneous emission, shows that QED is the superior theory. In Schrödinger"s treatment of the Compton effect the Planck constant is naturally introduced via the electron wavefunctions. The Bragg condition (I)-(3) not only ensures momentum conservation in frame S', it also shows that to the electron momentum there is a corresponding momentum of the radiation field. Thereby energy ћω'o and momentum ћω'o/c should not be considered as pertaining to a quantum but rather to a tantum, introduced by Dodd (1983). The ratio of energy and momentum in the radiation field can be obtained in classical electrodynamics.
fact that this is not the case for some processes, e.g. spontaneous emission, shows that QED is the superior theory. In Schrödinger"s treatment of the Compton effect the Planck constant is naturally introduced via the electron wavefunctions. The Bragg condition (I)-(3) not only ensures momentum conservation in frame S', it also shows that to the electron momentum there is a corresponding momentum of the radiation field. Thereby energy ћω'o and momentum ћω'o/c should not be considered as pertaining to a quantum but rather to a tantum, introduced by Dodd (1983). The ratio of energy and momentum in the radiation field can be obtained in classical electrodynamics.
 fact that this is not the case for some processes, e.g. spontaneous emission, shows that QED is the superior theory. In Schrödinger"s treatment of the Compton effect the Planck constant is naturally introduced via the electron wavefunctions. The Bragg condition (I)-(3) not only ensures momentum conservation in frame S', it also shows that to the electron momentum there is a corresponding momentum of the radiation field. Thereby energy ћω'o and momentum ћω'o/c should not be considered as pertaining to a quantum but rather to a tantum, introduced by Dodd (1983). The ratio of energy and momentum in the radiation field can be obtained in classical electrodynamics.
fact that this is not the case for some processes, e.g. spontaneous emission, shows that QED is the superior theory. In Schrödinger"s treatment of the Compton effect the Planck constant is naturally introduced via the electron wavefunctions. The Bragg condition (I)-(3) not only ensures momentum conservation in frame S', it also shows that to the electron momentum there is a corresponding momentum of the radiation field. Thereby energy ћω'o and momentum ћω'o/c should not be considered as pertaining to a quantum but rather to a tantum, introduced by Dodd (1983). The ratio of energy and momentum in the radiation field can be obtained in classical electrodynamics.In Compton's treatment the response of a point charge to electromagnetic radiation is studied describing the motion of the charge using non-quantum mechanics and radiation using classical electrodynamics. The Planck constant has to be introduced in a separate step either by comparing the final equation with experimental results or directly with equation (6) (Dodd 1983). It is not surprising that in this case in additional ad hoc assumption has to be introduced.
It is taken that the oscillating electron does not radiate until being accelerated to rest longitudinally in the 'spatial' interaction frame. This is the more disturbing as only radiation reaction can accelerate it (Kallmann and Mark 1926).
It is of advantage to distinguish carefully the three levels Not distinguishing Schrödinger's and Compton's treatment may bewilder readers (Kidd el al 1985). Thus we could even establish a relativity principle of the philosophy of physics: a statement is meaningful only with respect to a theoretical background.
In conclusion, the treatment of the Compton effect in the semiclassical approximation is not suited for the main course of introductory quantum physics. Extensive use of special relativity in a quantum context may annoy students. Nevertheless, it appears interesting enough to be used occasionally as an advanced topic to show that the photon picture is not exclusive it: explaining the Compton effect. Reflections in the philosophy of physics may also not be appropriate for students but may be instructive for teachers.
Acknowledgments
This work was completed during a stay at the Institut fur Didaktik der Physik, Justus-Liebig-Universitat, Giessen, Federal Republic of Germany. Thanks are due to Professor W. Kuhn for hospitality and to Raziskovalna skupnost Slovenije for a grant.
References
Bambini A., Renieri A. and Stenholm S. 1979 Phys. Rev. A 19 2013-25.
Born M. and Wolf E. 1939 Principles of Optics (London: Pergamon) p.590.
Compton A.H. 1923 Phys. Rev. 21, 433-502
Dodd J.N. 1983 Eur. J. Phys. 4, 203-11
Döring W. 1973 Atomphysik una Quantenmechanik (Berlin: de Gruyter) p. 249
Hecht E. and Zajac A. 1979 Optics (Reading, Mass.: Addison-Wesley) p. 3 97
Kallmann H. and Mark H. 1926 Erg. ex. Naturwiss. 5, 267-324
Kidd R. Ardini J. and Anton A. 1985 Am. J. Phys. 53, 641- 644
Kuhn W. and Stockier M. 1985 Praxis Naturwiss. 34, 25-37
Levy-Leblond J-M. 1936 Am. J. Phys. 44, 1130-2
Möller C. 1972, The Theory of Relativity (Oxford: Oxford University Press), p.60.
Srhrödinger E. 1927.4nn. Phys. 28, 257-64
Strnad J. 1986a Praxis Naturwiss, in press
—— 1986b Am. J. Phys. 54. 650-2

