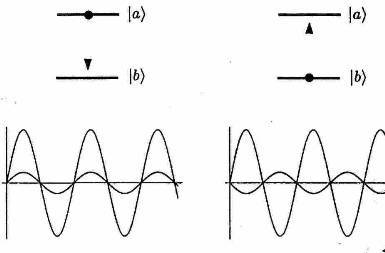
Рис.1. Слева: конструктивная интерференция излучения атомного диполя и падающей волны. Справа: деструктивная интtрференция индуцированного излучения и падающей волны.
М.О.Скалли, М.С. Зубайри [1] - Fig. 5.6.
М.О.Скалли, М.С. Зубайри [1] - Fig. 5.6.



М.О. Скалли.
М.С. Зубайри



Джордж Гринштейн
Артур Зайонц

Уильям Лэмб и Марлан Скалли. Хьюстон, 1992
«КВАНТОВЫЕ СКАЧКИ» – ПРЕДРАССУДОК РАННЕЙ КВАНТОВОЙ ТЕОРИИ. Л.Р.
Если электрон как целое «прыгает» с одного уровня на другой, то справедлив «парадокс Планка» – невозможность регистрации слабого излучения квантовым приемником – для накопления атомом энергии hν нужно слишком много времени.

Планк указал на следующий парадокс, связанный с регистрацией электромагнитного излучения квантовым детектором.
Пусть для наблюдения используется фотоумножитель с потенциалом выхода фотокатода U(ν). Предположим, что один эмиттирующий электрон собирает энергию излучения с площади взаимодействия Sо, равной по порядку величины площади единичного электронного цуга внутри кристаллической решетки фотослоя. Если же эмиттирует не свободный, а связанный электрон, то Sо совпадает с площадью внешней оболочки атома.
Время, за которое энергия hν=еU(ν) сможет быть накоплена атомным электроном, определяется как
T= hν/JSо
Полагая J = 10(-22) вт/см² (предел чувствительности современных квантовых приемников), при hν = 2эв = 3,2х10(-19)дж, Sо = 10(-16) см², получим для времени ожидания сигнала абсурдно большое значение
T ≈ 3х10(19) сек
В действительности, как мы покажем ниже, экспериментально наблюдаемый средний промежуток времени между двумя фотоотсчетами при такой интенсивности излучения оказывается по крайней мере на 14 порядков ниже.
Так называемая «редукция волновой функции» в момент регистрации, предполагаемая копенгагенской трактовкой квантовой механики, происходит не в реальной действительности, а только в сознании наблюдателя и эта мысленная редукция никак не объясняет, каким образом распределенная по большому объему энергия излучения может сконцентрироваться в объеме единичного атома.
Покажем, что все это рассуждение основано на неверных предпосылках и полностью теряет силу в свете современных представлений о взаимодействии излучения с атомом.
Если на двухуровневую систему действует монохроматическое внешнее поле излучения, то система начинает осциллировать с частотой Раби
Ω = Ed/ћ (1)
где Е – амплитуда поля, d – дипольный момент между двумя уровнями.
При этом населенность верхнего уровня (при условии точного резонанса внешнего поля с разностью частот между уровнями) определяется как (см., напр. [1] - §5.2.1 или [2] - §5.1):
W = sin²( Ωt/2) (2)
При этих переходах атом обменивается энергией с внешним полем: в первом полупериоде атом забирает энергию у поля, во втором – отдает ее обратно. Это происходит потому, что при переходе сверху вниз индуцированное излучение атома находится в фазе с падающим излучением, при переходе снизу вверх - в противофазе (Рис.1).
Никаких «скачков» электронной плотности при этом не происходит, вопреки тем представлениям, которые бытовали на первых этапах развития квантовой теории. Переходы электронной плотности между стационарными состояниями носят постепенный, непрерывный характер.
Переходы сверху вниз происходят не только под действием внешнего поля, но под действием полей окружающих атомов (столкновения) или вакуумного поля (спонтанные переходы). При этом подавляющая часть таких переходов имеет характер тепловой релаксации, когда энергия верхнего уровня безизлучательно передается окружающим атомам. Регистрация излучения детектором может иметь место лишь в тех сравнительно редких случаях, когда переход сверху вниз происходит с излучением фотона (волнового цуга), некогерентного внешнему полю или с отрывом электронного облака от атома (фотоэффект).
Рассмотрим с этих позиций описанный выше «парадокс Планка».
Когда фронт излучения достигает поверхности детектора, начинается одновременная осцилляция всех атомов с частотой Раби. В силу появления возбужденных состояний, возникает определенная вероятность актов регистрации излучения, которая пропорциональна произведению средней населенности верхнего уровня Wср на число возбужденных атомов n .
Р ~ Wср n (3)
Планк рассматривает случай, когда Е очень мало: в этом случае очень мала будет и частота Раби, т.е.
Ωτ <<1 (4)
где τ – время тепловой релаксации, в твердом теле имеющее порядок 10(-13) сек.
Таким образом, при малой интенсивности внешнего излучения верхние уровни успевают заселиться за время тепловой релаксации лишь до ничтожно малого значения.
Согласно (2), средняя населенность верхнего уровня может быть оценена как
Wср ≈ (Ωτ)²/4 (5)
Соответственно, с возбужденного уровня может быть оторвана только та часть электронной плотности, которая на этом уровне находится. Соответственно, если регистрируется вторичное излучение, то интегральная интенсивность испускаемого цуга пропорциональна населенности верхнего уровня. При этом все частотные условия фотоэффекта остаются в силе.
Приведем численный пример. С учетом того, что E = √2πJ/с, для интенсивности падающего излучения J = 1 вт/см² частота Раби составит
Ω ≈ 3х10(7)гц . Принимая время тепловой релаксации τ = 10(-13)сек, получим из (5) Wср ≈ 10(-11). Для предельно малой интенсивности, которую удается регистрировать на сегодняший день, J = 10 (-22) вт/см², имеем значение
Wср ≈ 10(-33).
Итак, в каждом единичном акте регистрации участвует электронный или фотонный цуг очень малой интегральной интенсивности, по сравнению с интегралом от |ψ|² для полностью заполненного уровня.
Однако, благодаря очень большому числу атомов n, одновременно взаимодействующих с излучением, число отсчетов детектора N(t) за время наблюдения t достаточно велико и определяется интегральным соотношением, вытекающим из закона сохранения энергии:
N(t) = η JSt/hν (6)
где J – интенсивность падающего излучения, S – рабочая площадь детектора, η – квантовый выход регистрирующего устройства в целом.
Средний промежуток времени tср между последующими отсчетами (при условии, что tср много меньше разрешающего времени системы отсчета), можно определить, положив N(t) = 1. Тогда для J = 10(-22) вт/см² и
hν = 2 эв, получим tср ≈ 10(5) сек, что и определяет предельную чувствительность детектора, ограниченную минимально достижимой скоростью счета шумовых импульсов.
Вывод: никакого парадокса в регистрации сверхслабого излучения квантовым приемником в действительности нет.
Кажущаяся парадоксальность картины, нарисованной Планком, вызвана ошибочным предположением (общепринятым в 1920-40-е годы), что каждый раз в акте регистрации участвует «целый» электронный или фотонный цуг с полной энергией ћω, тогда как в действительности регистрируются цуги с энергией Wср ћω, где Wср <<1. Поэтому, вопреки рассуждению Планка, нет необходимости в «накоплении» энергии ћω в объеме единичного атома. Однако за среднее время тепловой релаксации τ атом успевает заимствовать у падающего излучения энергию Wср ћω, которая и передается детектору в единичном акте регистрации.
Еще раз подчеркнем, что условия резонанса или наличие частотной границы фотоэффекта связаны только с ω, тогда как величина Wср никак на эти условия не влияет.
[1] М.О.Скалли, М.С.Зубайри. Квантовая оптика. М. 2003.
[2] Д.Н.Клышко. Физические основы квантовой электроники. М. 1986.
Л.Регельсон, Москва, март 2010 г.

